Btrust Builders

Schnorr and Steady Wins the Race: The Case for Batch Validation

Understanding BIP340 Schnorr Signature Verification

Btrust Builders

Jun 23, 2025 — 11 min read

Written by Oghenovo Usiwoma

Note: All scripts used in this article are available on Github.

Introduction

BIP340 introduced Schnorr signatures to Bitcoin, offering several advantages over ECDSA.

One key benefit is its linear signature equation, which is easier to analyse and has been proven secure. Schnorr signatures are also non-malleable by default; that is, given a valid signature for a message, an adversary cannot generate another valid signature for the same message.

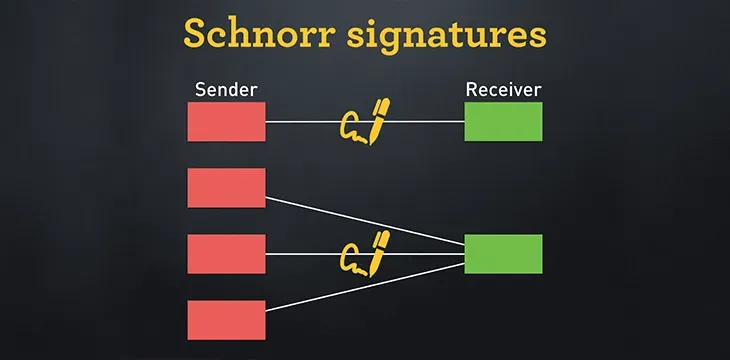
The linear nature of Schnorr signatures also enables efficient and private multisignatures, as well as batch verification.

Taproot, introduced in BIP341, is a SegWit version 1 output type that leverages Schnorr’s linear properties to unify pay-to-pubkey and pay-to-scripthash policies, making them indistinguishable until spent.

As Taproot adoption grows, Schnorr-based schemes—such as Silent Payments for privacy and MuSig and FROST for multi-signature schemes—will become more widely used, making efficient signature verification even more critical.

This article explores the mechanics of batch verification, presents benchmark results, and examines its potential impact on Bitcoin Core’s ConnectBlock() function—which is where transaction signature verification happens.

This article assumes that you have an understanding of Elliptic Curve mathematics and you are familiar with BIP340. If you need a refresher, check out Elliptic Curve Concepts for Bitcoin Developers.

Understanding BIP340 Schnorr Signature Verification

In Bitcoin, a signature is a piece of data that proves the owner of a transaction's inputs indeed authorised the transaction and that it has not been altered. Such a signature is generated using a cryptographic key pair:

Private Key – Kept secret by the owner(s) of the transaction inputs and used to create the signature.
Public Key – Included in the transaction input and used by others to verify the signature, ensuring the transaction's authenticity.

A BIP340 Schnorr signature consists of three components:

A message m
A public key P = dG, where d is the private key and G is the generator point of the elliptic curve
A signature (r, s), where:
- A nonce k is randomly chosen.
- The nonce commitment R = kG, and its x-coordinate, r = x(R) is used in the signature.
- The challenge is computed as e = Hash(r || x(P) || m).
- The signature scalar is s = k + ed (mod n), where n is the curve's order.

Signature Verification:

To verify the signature (r, s), we:

Recompute the challenge: e = Hash(r || x(P) || m)
Reconstruct the point R: R' = sG - eP
Check if the x-coordinates match:

If x(R') = r, the signature is valid.

This verification works because:

sG = (k + ed)G = kG + e(dG) = R + eP

Rearranging gives:

R = sG - eP

Since R' is computed the same way during verification, the signature is valid if x(R') = r.

The Mechanics of Batch Verification

Given the number u of Schnorr signatures:

Messages: m_1, m_2, ..., m_u
Signatures: (r_1, s_1), (r_2, s_2), ..., (r_u, s_u)
Public keys: P_1, P_2, ..., P_u

Batch verification allows us to validate all signatures simultaneously, reducing computational costs compared to verifying each one separately. Instead of checking each signature individually:

s_i G = R_i + e_i P_i for each i = 1, ..., u

We instead compute a single equation

Compute Challenges

For each signature, compute the challenge:

e_i = H(r_i || x(P_i) || m_i)

Compute the Batch Equation

Instead of verifying each signature separately, we check whether:

(s_1 + s_2 + ... + s_u)G = R_1 + e_1 P_1 + R_2 + e_2 P_2 + ... + R_u + e_u P_u

Using Strauss’ Multi-Scalar Multiplication algorithm

We can take this verification a step further. Suppose we need to compute the sum of two scalar multiplications:

k_1 * P_1 + k_2 * P_2

We could perform each scalar multiplication and sum them but, various algorithms can do this faster. One such algorithm is Strauss’ Multi-Scalar Multiplication algorithm (MSM) also known as Shamir’s trick, which speeds up this computation by lining up the two scalars and processing their bits simultaneously.

To do this, start by initialising an accumulator to the “Point at Infinity”. For each bit position, i:

If both bits of k1_i and k2_i are zero, double the current accumulator value
If k1_i = 1 and k2_i = 0, double the current accumulator value and add P1
If k1_i = 0 and k2_i = 1, double the current accumulator value and add P2
If both are 1, double the current accumulator value and add P1 + P2

After all bits are processed, the current accumulator value is the result. This approach can be generalised to n scalar multiplications.

Our current Batch Verification equation will require us to do two MSMs. We can thus rewrite the equation so we only have to do one:

0 = R_1 + e_1 P_1 + R_2 + e_2 P_2 + ... + R_u + e_u P_u - (s_1 + s_2 + ... + s_u)G

If this equation holds, all signatures are valid.

Preventing Attacks with Random Scalars

The above equation is vulnerable because an attacker could craft an invalid signature that cancels out errors in another. To prevent this, we must introduce random scalars c_1, c_2, ..., c_u, chosen randomly for each batch verification.

To improve the computation speed, set c_1 = 1, which modifies the equation to:

0 = R_1 + e_1 P_1 + c_2(R_2 + e_2 P_2) + ... + c_u(R_u + e_u P_u) - (s_1 + c_2 s_2 + ... + c_u s_u)G

These scalars ensure invalid signatures cannot be manipulated to pass batch verification.

Efficiency Gains

Each Schnorr signature verification requires two elliptic curve (EC) scalar multiplications, one to compute sG and another to compute eP. Thus, verifying u signatures independently requires:

2u EC scalar multiplications

Batch verification reduces the number of scalar multiplications by combining all signatures into a single equation. The original batch equation requires:

1+u EC scalar multiplications

However, the modified batch equation introduces random scalars c_2, ..., c_u which means that R_2, ..., R_u are multiplied by additional scalars, which increases the total count back to:

2u EC scalar multiplications

At first glance, this might seem like batch verification does not save computation. However, we can optimise the computation using the efficient multi-scalar multiplication techniques discussed earlier. For example, instead of performing 2u separate scalar multiplications and then summing the results, Strauss’ algorithm allows us to compute multiple EC scalar multiplications more efficiently.

Take for example the batch verification implemented here which applies Strauss’ algorithm. We can observe practical speedups over individual verification, especially when verifying a large number of signatures.

**Efficiency gains of the batch Schnorr signature verification** **implementation****.This implementation verifies 53 signatures at a time.**

Batch Tweak Checks

A Tweaked Taproot output is derived from an internal public key and a tweak t. This allows for spending conditions that either reveal the internal key (key spend) or prove a script path (script spend).

To compute the tweaked public key:

Convert the tweak t (a scalar) into a public key by computing: T = tG
Add this to the internal public key P to get the tweaked key Q: Q = P + tG

When spending via a script path, the spender must prove that the given internal public key and tweak reconstruct the Taproot output key. This means recomputing Q from (P, t) and checking if it matches the output being spent.

Since computing tG requires one elliptic curve (EC) scalar multiplication per tweak, verifying multiple tweaks individually can be computationally expensive.

Batching Tweak Checks

We can apply the same efficient multi-exponentiation techniques used for batch Schnorr signature verification to speed up tweak checks. Instead of verifying each tweak separately, we validate all tweaks with a single equation:

Given Inputs

Internal public keys: P_1, P_2, ..., P_u
Tweaks: t_1, t_2, ..., t_u
Tweaked public keys: Q_1, Q_2, ..., Q_u

Construct the Batch Equation

Rewriting Q_i = P_i + t_i G, we define:

t_iG = Q_i - P_i

The equation to batch verify tweak is given as:

(t_1 + t_2 + ... + t_u)G = Q_1 - P_1 + Q_2 - P_2 + ... + Q_u - P_u

To make use of Strauss' multi-scalar multiplication algorithm, we rewrite the equation as:

0 = P_1 - Q_1 + P_2 - Q_2 + ... + P_u - Q_u + (t_1 + t_2 + ... + t_u)G

We define:

Z_i = P_i - Q_i

Thus, the equation for all tweaks simplifies to:

0 = Z_1 + Z_2 + ... + Z_u + (t_1 + t_2 + ... + t_u)G

If this equation holds, all tweaks are valid.

Preventing Attacks with Random Scalars

To prevent attackers from crafting invalid tweaks that pass batch verification, we introduce random scalars c_2, ..., c_u. The modified equation becomes:

0 = Z_1 + c_2 Z_2 + ... + c_u Z_u + (t_1 + c_2 t_2 + ... + c_u t_u)G

By applying Straus’s algorithm (as used in batch signature validation), we can efficiently compute these EC scalar multiplications in batches, improving performance when processing entire blocks.

**Efficiency gains of the batch tweak check** **implementation****.This implementation can check 106 tweaks at a time.**

Impact on Bitcoin Core’s `ConnectBlock()` Performance

To estimate the theoretical performance improvement from implementing batch verification in Bitcoin Core, we need to quantify how much time Schnorr signature verification contributes to the overall ConnectBlock() execution time.

1. Establishing a Baseline (D_o)

First, we run a ConnectBlock() benchmark to measure the default block validation rate, D_o (ns/block), which includes all validation steps, including Schnorr signature verification.

2. Measuring Execution Without Schnorr Signature Verification (D_eo)

Next, we disable Schnorr signature verification and re-run the ConnectBlock() benchmark. This gives us a new measurement, D_eo, representing the block validation duration without Schnorr signature checks.

3. Computing the Time Spent on Schnorr Signature Verification (D_to)

The difference between the two measurements,

D_{to} = D_o - D_{eo}

represents the portion of ConnectBlock() time spent on Schnorr signature verification.

4. Estimating Performance Improvement

If batch verification improves Schnorr signature verification by 20%, then the expected improvement in ConnectBlock() can be estimated as:

Performance Gain = ((0.2 × Dto) / Do) × 100%

This formula expresses the percentage reduction in block validation duration due to the reduced cost of Schnorr signature verification.

Experimentation

To measure the potential performance improvements from batch verification in Bitcoin Core, we conducted benchmarks using a modified version of Bitcoin Core. These benchmarks compare ConnectBlock() performance with and without Schnorr signature verification.

1. Benchmarking Fully Schnorr-Signed Blocks

We first evaluate the worst-case scenario—blocks filled with Schnorr signatures.

Baseline Performance (D_o)

We run the benchmark using two script verification threads:

> build_dev_mode/src/bench/bench_bitcoin -filter=ConnectBlockAllSchnorr

ns/block	block/s	err%	ins/block	cyc/block	IPC	bra/block	miss%	total	benchmark
66,833,032	14.96	0.3%	703,740,094	227,566,928	3.092	17,447,766	1.6%	0.74	ConnectBlockAllSchnorr

This gives us D_o = 66,833,032 ns/block.

Measuring Execution Without Schnorr Signature Verification (D_eo)

Next, we disable Schnorr signature verification and rerun the benchmark:

> build_dev_mode/src/bench/bench_bitcoin -filter=ConnectBlockAllSchnorr -disableschnorr

ns/block	block/s	err%	ins/block	cyc/block	IPC	bra/block	miss%	total	benchmark
13,463,376	74.28	0.3%	130,734,364	45,727,408	2.859	7,547,020	0.3%	0.15	ConnectBlockAllSchnorr

This gives us D_eo = 13,463,376 ns/block.

Computing the Performance Impact of Schnorr Signature Verification

We calculate the portion of ConnectBlock() execution time dedicated to Schnorr signature verification:

D{to} = 66_883_032 - 13_463_376

Performance Gain = ((0.2 x 53_419_656) / 66_883_032) x 100%

Performance Gain = 15.97%

This means that batch verification could reduce block validation time by approximately 16% for fully Schnorr-signed blocks when using two script verification threads.

2. Benchmarking Mixed ECDSA/Schnorr Blocks

Next, we analyse a more typical block composition—20% Schnorr signatures and 80% ECDSA signatures, reflecting Bitcoin's current transaction mix.

Baseline Performance (D_o)

We run the benchmark on mixed-signature blocks:

> build_dev_mode/src/bench/bench_bitcoin -filter=ConnectBlockMixedEcdsaSchnorr

ns/block	block/s	err%	ins/block	cyc/block	IPC	bra/block	miss%	total	benchmark
83,963,387	11.91	0.2%	880,597,181	285,806,808	3.081	22,034,984	1.6%	0.93	ConnectBlockMixedEcdsaSchnorr

This gives us D_o = 83,963,387 ns/block.

Measuring Execution Without Schnorr Signature Verification (D_eo)

Disabling Schnorr signature verification:

> build_dev_mode/src/bench/bench_bitcoin -filter=ConnectBlockMixedEcdsaSchnorr -disableschnorr

ns/block	block/s	err%	ins/block	cyc/block	IPC	bra/block	miss%	total	benchmark
70,759,019	14.13	0.1%	738,978,882	240,260,166	3.076	19,649,017	1.4%	0.78	ConnectBlockMixedEcdsaSchnorr

This gives us D_eo = 70,759,019 ns/block.

Computing the Performance Impact of Schnorr Signature Verification

D{to} = 83_963_387 - 70_759_019

Performance Gain = ((0.2 x 13_204_368) / 83_963_387) x 100%

Performance Gain = 3.15%

This means that batch verification could reduce block validation time by approximately 3% for Bitcoin blocks with a typical mix of ECDSA and Schnorr signatures.

Conclusion

For fully Schnorr-signed blocks, batch verification could reduce ConnectBlock() execution time by ~16%.
For typical Bitcoin blocks (20% Schnorr, 80% ECDSA), the improvement is ~3%.
These optimisations could significantly improve node efficiency as Schnorr adoption increases.

Impact on current IBD performance

To estimate the potential performance impact on current IBD, we use Benchcoin to measure IBD duration with Schnorr signature verification and assumevalid disabled.

**Results from Benchcoin. “Mainnet-Default” uses a 450MiB dbcache and “Mainnet-Large” uses a 32000MiB dbcache.**

We observe a 14.4% speedup with Schnorr signature verification disabled. We expect batch verification to shave off 20% of Schnorr signature verification time.

Computing the Performance Impact of Schnorr Signature Verification

Performance Gain = 0.2 x 14.4 x 100%

Performance Gain = 2.88%

This means that batch verification could reduce IBD time by 2.88%. The improvement becomes more significant as Schnorr signatures replace ECDSA over time.

Implications for the future

The increasing adoption of Schnorr signatures is expected to reshape Bitcoin’s transaction landscape. The pie chart below illustrates the current distribution of script types in the UTXO set, while the stacked bar chart shows how this distribution evolves as a function of block height.

**Distribution of script types in the UTXO set at height 884446.The UTXO set distribution shows that 33% of UTXOs use Witness_v1_Taproot.**

**Distribution of script types by block height in the UTXO set at height 884446.**

Over time, we can expect that several emerging technologies, such as the following, to drive more Schnorr signature adoption:

1. Silent Payments

Silent Payments is a privacy-enhancing payment mechanism that relies on the linearity of Schnorr signatures to generate unique scriptPubKeys for recipients based on transaction input data and a Silent Payment address.

Unlike static reusable payment addresses, Silent Payments derive fresh Taproot outputs for each payment, making transaction linkage difficult.
As adoption grows, it will directly increase the use of Schnorr signatures, which are essential to its cryptographic construction.

2. MUSIG2 and FROST

MuSig2 and FROST enable efficient multi-signature aggregation using Schnorr signatures. These schemes allow multiple parties to collaboratively sign transactions while producing a single aggregated public key that appears indistinguishable from a standard Taproot output.

Current Multisig UTXO Share:
- 8.8% of the UTXO set consists of P2SH and P2WSH outputs.
- These are likely multisig scriptPubKeys, which traditionally use ECDSA-based multisig schemes.
- MuSig2 and FROST could replace these methods, reducing on-chain footprint and improving efficiency.
Future Impact:
- As wallets integrate MuSig2/FROST, we expect a gradual shift from legacy multisig schemes to Taproot-based outputs, increasing Schnorr and Taproot adoption.

3. Covenants and Vaults

Covenants and vaults are mechanisms designed to restrict how coins can be spent, primarily for security and theft mitigation. Several proposed implementations leverage Schnorr signatures:

CHECKSIGFROMSTACK Simulation via Schnorr Tricks
- Some covenant proposals require CHECKSIGFROMSTACK, an opcode that allows verification of arbitrary transaction data.
- Schnorr signature tricks can simulate this functionality, making certain covenants possible without soft forks.
- MuSig2 and FROST could replace these methods, reducing on-chain footprint and improving efficiency.
OP_VAULT and Taproot-Based Vaults
- OP_VAULT introduces a script-based vaulting mechanism that allows pre-specified spending conditions.
- Taproot enables vault transactions to appear as regular single-sig outputs unless conditions are triggered.
- This enhances privacy and reduces on-chain footprint while providing theft resistance.

Conclusion

As explored, batch verification of Schnorr signatures offers a significant improvement in Bitcoin’s Block verification process. By reducing the computational cost of verifying multiple signatures, batch verification enhances node performance, accelerates block validation, and optimizes Initial Block Download (IBD) duration.

The benchmarks explored earlier demonstrate that:

Bitcoin Core’s ConnectBlock() performance could improve by ~16% for fully Schnorr-signed blocks and ~3% for typical blocks.
IBD duration could be reduced by ~2.88%, improving full-node synchronization speeds.
Multisig, privacy, and security enhancements—technologies like MuSig2, FROST, Silent Payments, and Vaults—will further drive Schnorr adoption, making batch verification increasingly beneficial.

As Bitcoin adoption grows and Taproot-based features become more widespread, the efficiency gains from batch verification will play a crucial role in scalability, decentralization, and long-term network sustainability.